본 웹사이트에 게시된 모든 콘텐츠*는 저작권 소유자의 재산이며 저작권법에 의해 보호됩니다.
무단 수정 및 배포 또는 상업적 이용을 금지합니다.
* : 별도의 출처가 표기되지 않은
오늘은 제가 음향학을 공부하며 직관적으로 이해하기 어려웠던 부분 중 하나를 여러분과 나눠보고자 합니다.
바로 스피커의 저음 포트에 대한 이야기입니다.
많은 스피커 제품이 포트형 디자인을 채택하고 있으므로, 이는 스피커를 공부하며 피해가기 어려운 주제라고 생각합니다.
그리고 스피커의 포트가 바로, 헬름홀츠 공명기입니다.
시작합시다.
공진주파수
우선 진동계의 고유진동수 공식과 그 물리적 의미에 대해서 알아봅시다.
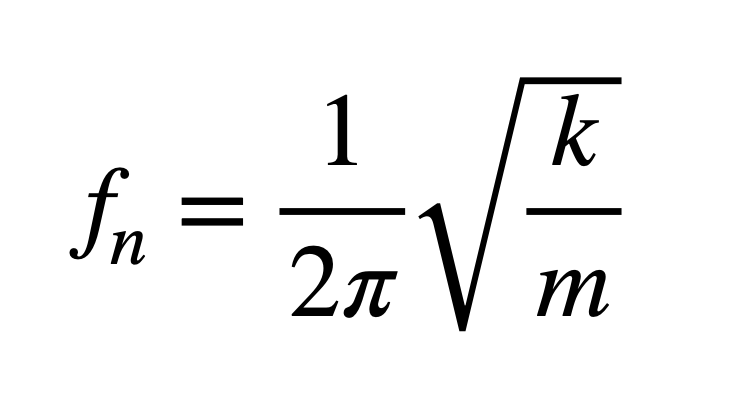
fn은 고유진동수, m은 질량, k는 스프링의 강성을 의미합니다.
수식이 낯설더라도 괜찮습니다.
이 식은 고유진동수 fn 에 대해서, 스프링이 단단해질수록 높아지고, 진동계의 질량이 무거워질수록 낮아진다는 것을 설명하고 있습니다.
(수식에 따르면 k가 증가하면 fn은 증가하고, m이 증가하면 fn은 감소합니다.)
이를 우리에게 좀 더 친숙한 스피커 드라이버의 상황으로 가져와 생각해봅시다.
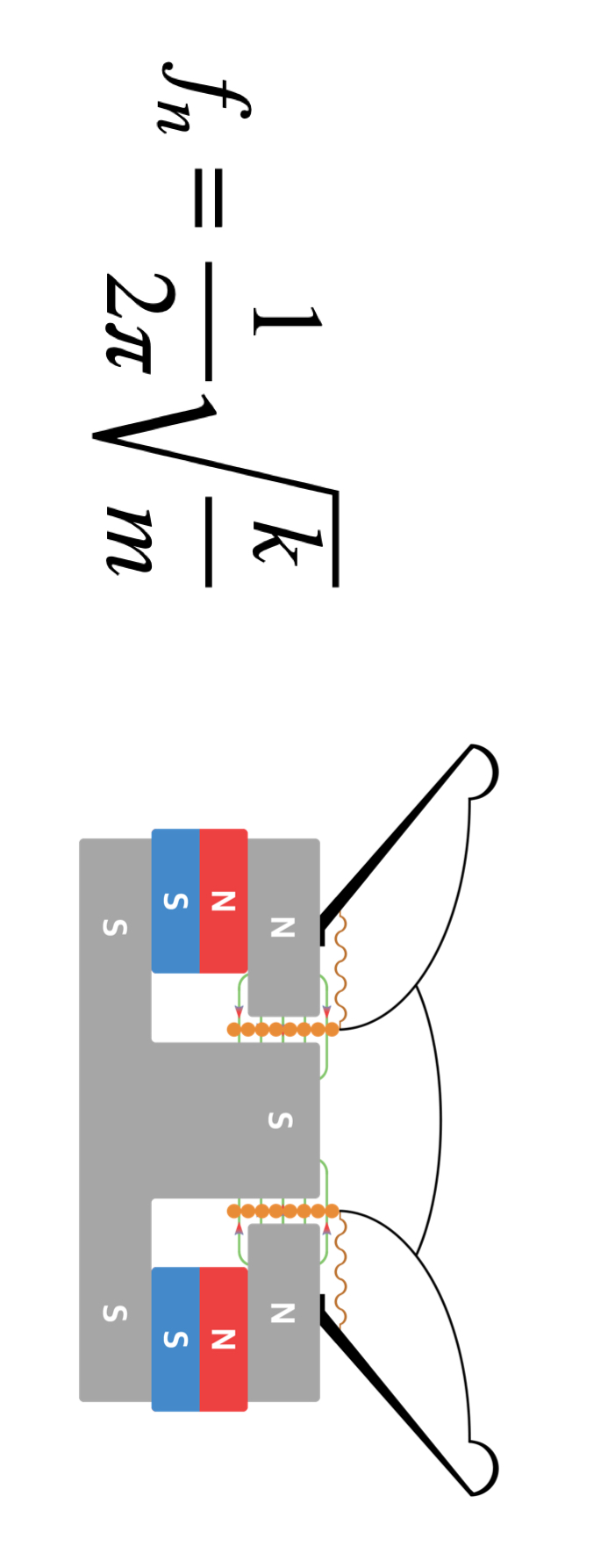
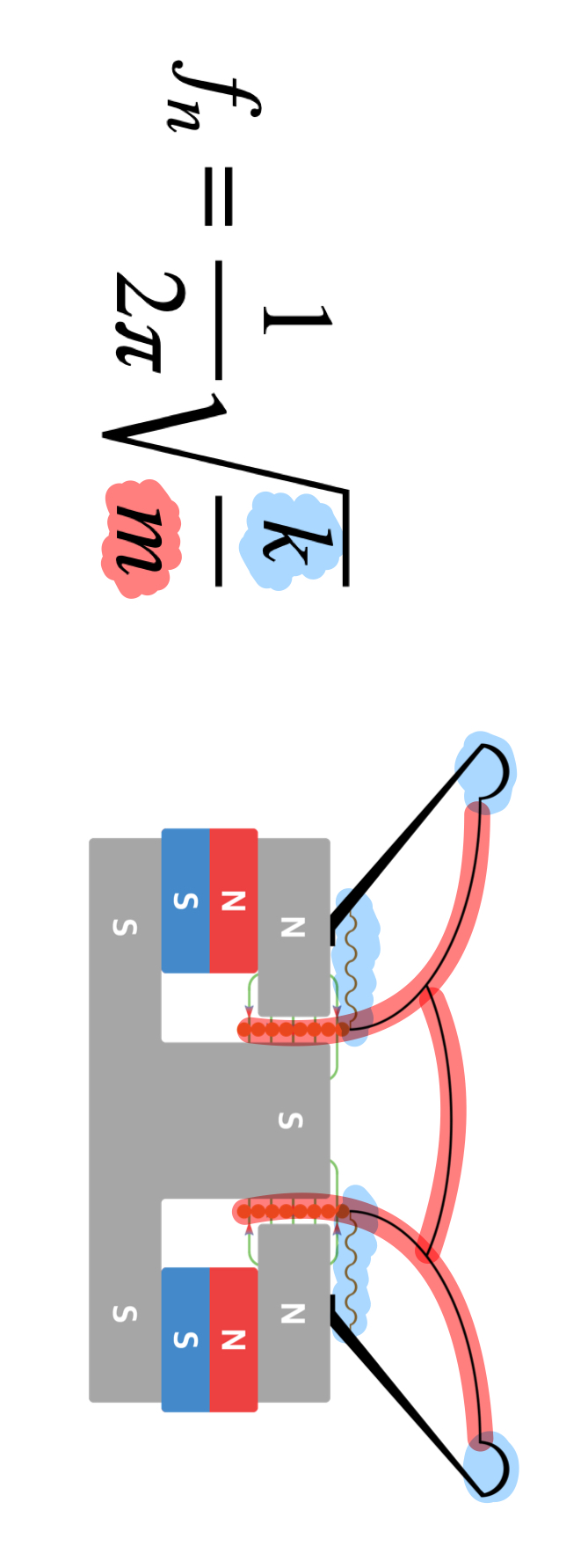
k는 스피커의 복원력을 담당하는 파트들, 그리고 m은 운동에 관여하는 모든 부분들의 질량을 의미합니다.
즉.
스피커 드라이버가 무거워지면 공진주파수는 낮아지고,
스피커 드라이버의 서스펜션 시스템이 단단해질수록 공진주파수는 높아진다는 의미입니다.
그리고 이것은 해당 스피커 드라이버의 저주파수 하한을 결정하는 지배적인 요인이 됩니다.
헬름홀츠 공명기
이제 오늘의 주인공인 헬름홀츠 공명기의 공명주파수 공식을 소개하겠습니다.
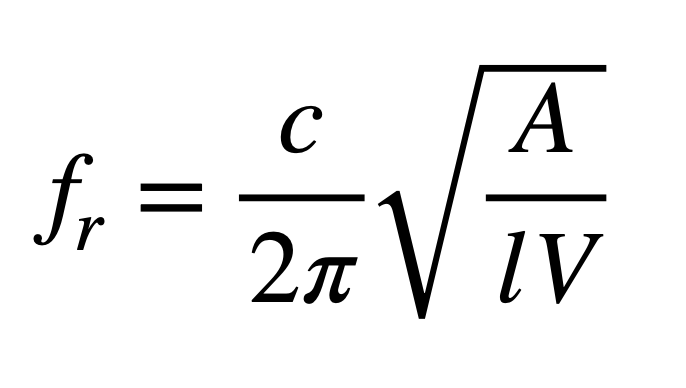
한 눈에 보아도 식의 구조가 상당히 닮아있다는 것을 알아챌 수 있습니다.
c 는 음속,
A 는 포트의 단면적,
l 은 포트의 길이,
V 는 박스 내부 공기의 체적입니다.
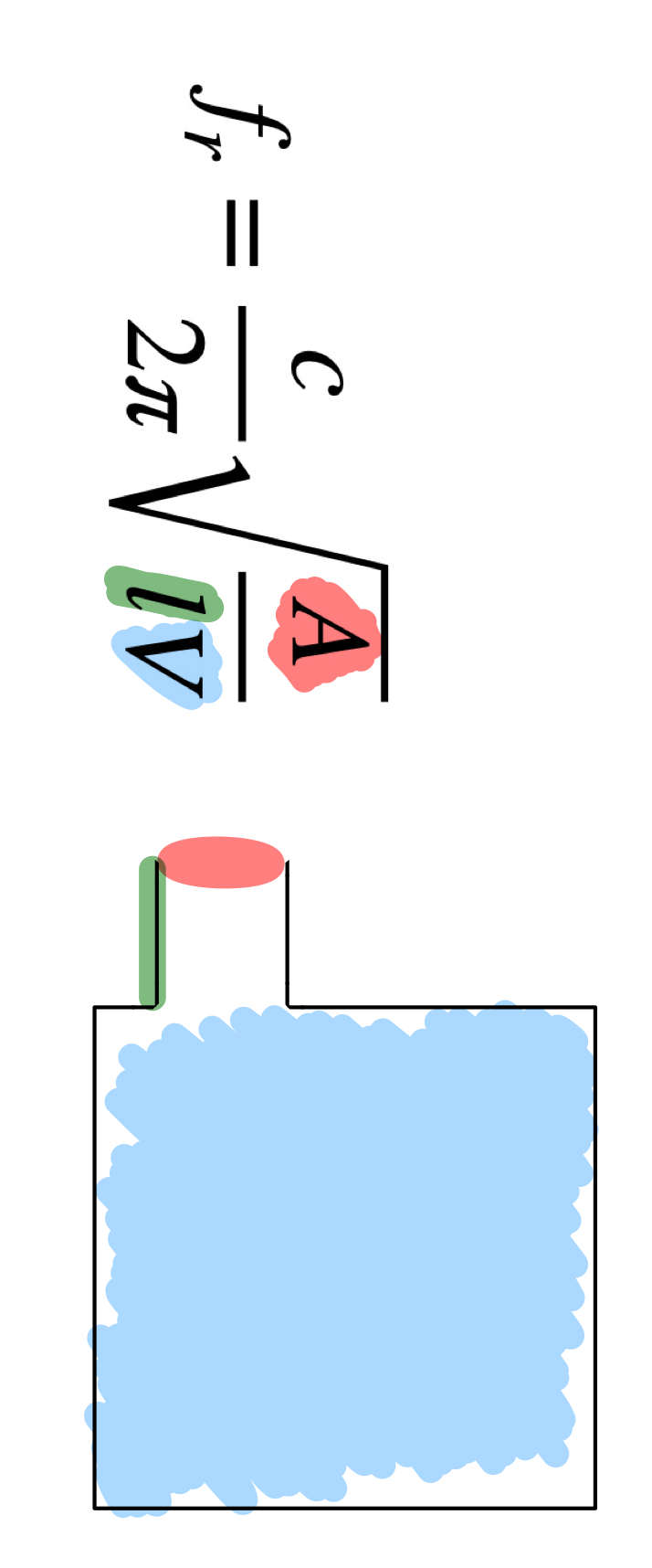
우리는 이 포트(헬름홀츠 공명기)의 구조가 스피커 드라이버와 사실상 구조가 동일하다고 배우곤 합니다.
포트 내부의 공기를 진동계의 m(질량)으로, 박스 내부의 공기를 k(스프링)로 생각하면 이해하기 쉽기 때문입니다.
그래서 동일한 식을 이용해 스피커 포트를 이렇게 설명합니다.
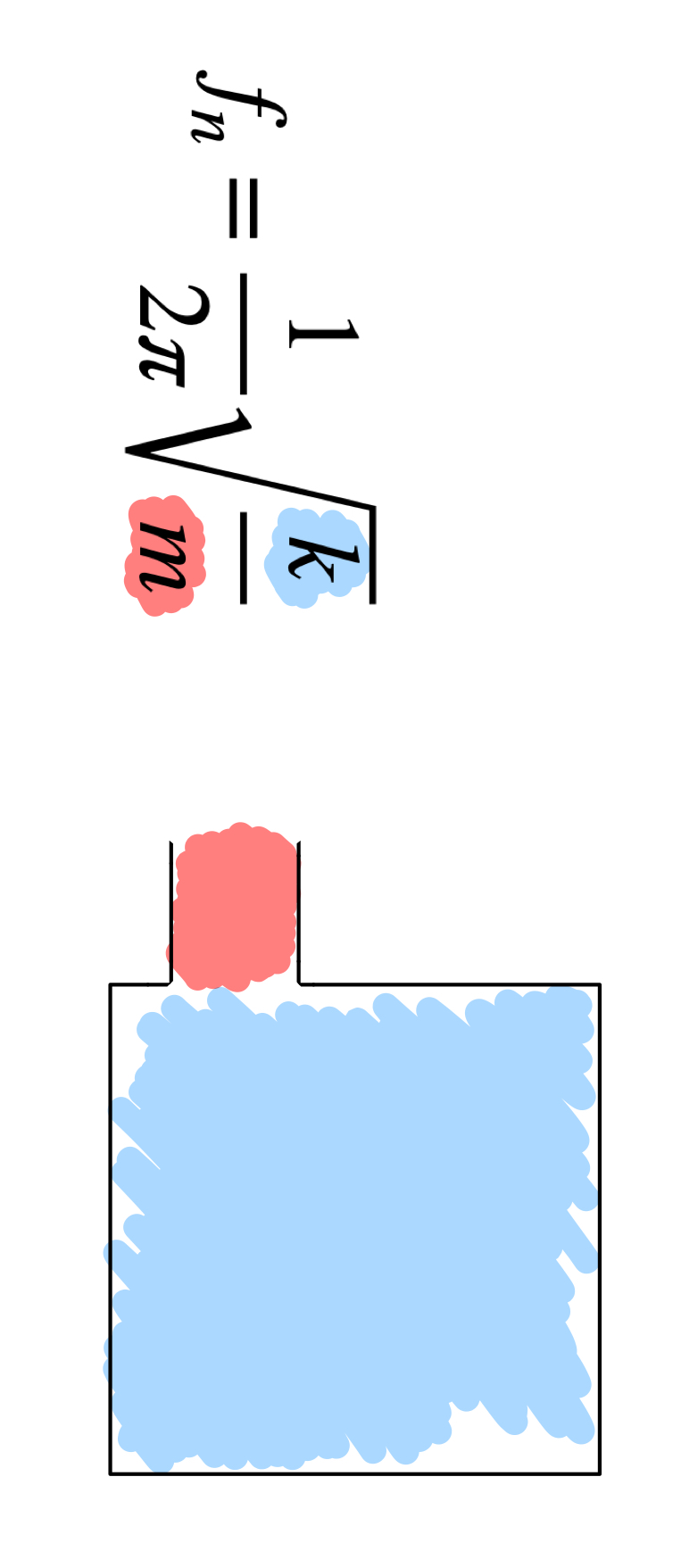
하지만 그렇게 생각하면 식에서 이상한 점을 몇 가지 발견할 수 있는데요, 사실 이 글의 주제가 바로 여기서부터 시작합니다.
의문점 <1>
분명히 공기 체적V는 스프링 k에 해당하고, 포트 내 공기(단면적 A 곱하기 길이 l)는 질량 m에 해당한다고 했는데,
진동계 고유진동수 식의 루트항
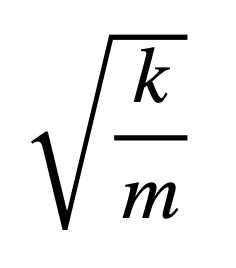
에서는 분모에 m이 있고, 분자에 k가 있습니다.
하지만 헬름홀츠 공명기의 식 루트항
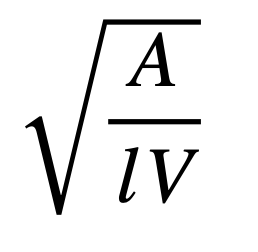
에서는 분모에 체적(스프링이라고 했던)에 해당하는 V가 있고, 포트 내 공기(질량)에 해당하는 A와 l은 서로 분리되어 있습니다.
의문점 <2>
포트의 단면적(A)이 증가한다는 것은, 포트 내부 공기의 질량이 증가한다는 의미입니다.
질량 m이 증가하면 분명 공진주파수는 감소해야하는데, 실제로는 A가 증가하면 공진주파수가 증가합니다.
즉, 포트의 직경이 커지면 공진주파수는 증가합니다.
분명 포트 내 공기의 질량도 증가할텐데 말입니다.
제가 마주쳤던 두 가지 혼돈이 바로 이것들이었습니다.
진동계의 공진주파수 식과 직관적으로 연결하기 어려웠고, 또한 현실에서 일어나는 현상과도 납득이 가지 않았습니다.
그래서 식을 유도해보기로 했습니다.
1.박스 내 체적 변화량
먼저, 스피커 박스 내 체적 변화량을 ΔV 로 약속합니다.
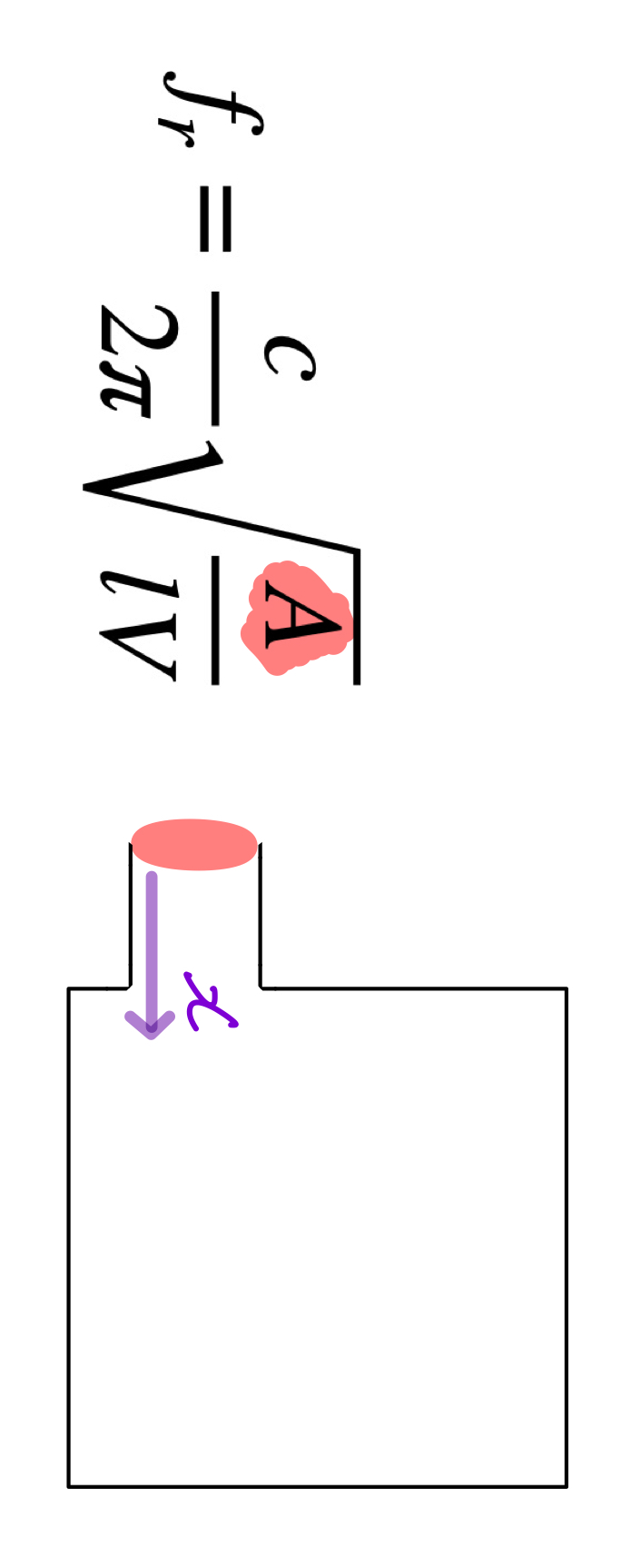
그러면 이는 포트의 단면적 A와, 포트 내부의 공기가 앞뒤로 움직이는 변위 x에 의해 결정될 것입니다.
얼만큼 넓은 면적으로(A), 얼만큼 깊게 압축하느냐(x)가 곧 내부 공기의 체적 변화량이 됩니다.
따라서
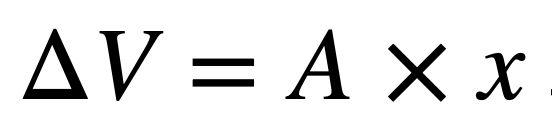
로 정리할 수 있습니다.
2.박스 내부의 압력 변화량
스피커 박스 내부의 압력 변화량을 ΔP 로 약속합니다.
스피커 박스 내부의 공기 압력이란 곧, 스피커 박스 내부의 공기가
“얼마나 딱딱한지” 를 의미합니다.
이는 공기의 압력에 대한 성질과 박스 내부 부피의 관계 및 그 부피의 변화량으로 나타낼 수 있으므로,
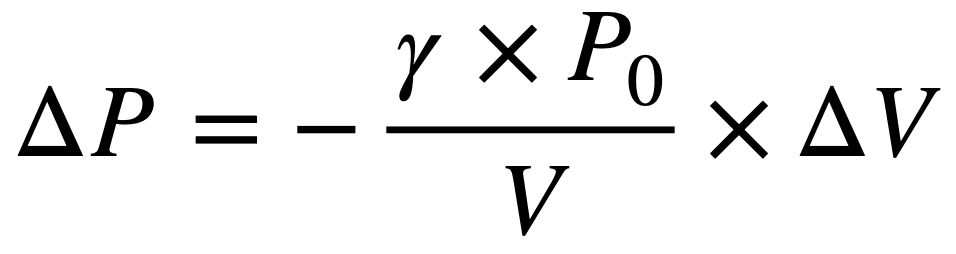
로 나타낼 수 있을 것입니다.
-> γ는 공기의 비열비, P0는 대기압입니다.
-> 이때 부호 마이너스(-)는 압력 변화의 ‘방향’을 나타냅니다. 기체는 부피가 줄어들면(-) 압력이 증가하기(+) 때문입니다.
3.스프링으로서 복원력
스프링으로서의 복원력을 F 로 약속합시다.
머릿속으로 떠올려보면, 공기 스프링의 복원력은 주사기(피스톤)의 압력 변화량과 단면적에 비례함을 알 수 있습니다.
즉,

로 나타낼 수 있습니다.
자 그런데 앞서 박스 내부의 압력 변화량을
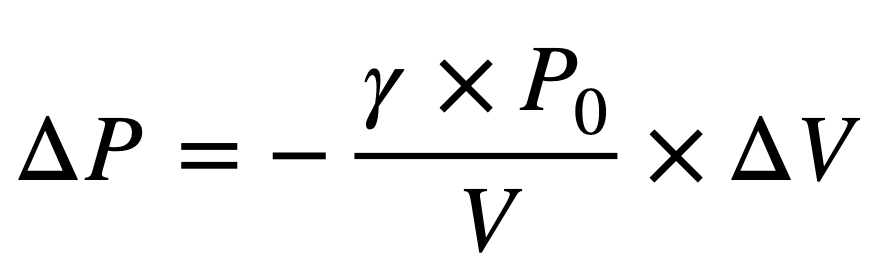
로 정리했으므로, 복원력은
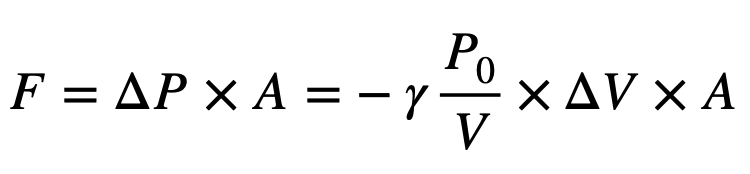
로 나타낼 수 있습니다.
그리고
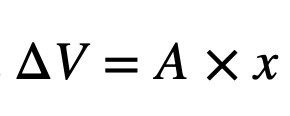
였으므로,
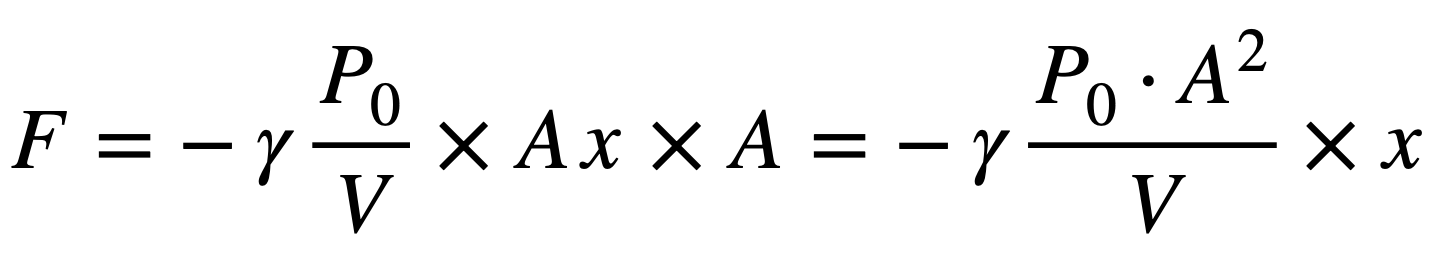
로 정리할 수 있습니다.
따라서 복원력 k는
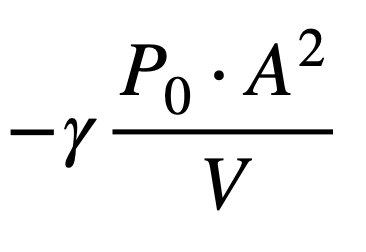
가 됩니다.
식을 정리해봅시다.
고생하셨습니다. 이제 각 요소의 물리적 의미를 따져보며 헬름홀츠 식을 다시 구성해봅시다.
포트 내부의 공기 질량 m은 공기의 밀도 ρ와 내부 부피를 곱한 값이므로,
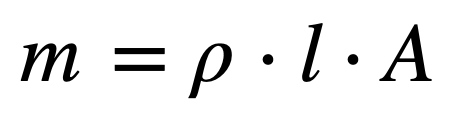
입니다.
스피커 박스 내부 공기의 스프링 상수 k는 앞서 정리한대로
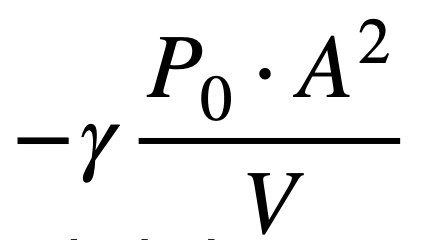
입니다.
-> 이때 복원력 크기의 절댓값을 다루기 때문에 앞으로 마이너스(-)는 생략해도 됩니다.
-> 힘의 방향은 고려하지 않습니다.
즉, 스피커 박스 내부 공기의 체적 탄성은
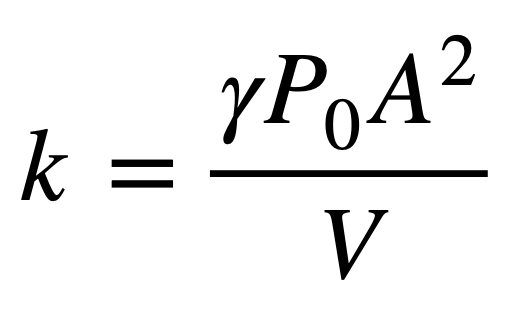
로 정리할 수 있습니다.
따라서 k와 m의 위치에 앞서 정리한 것들을 대입하면
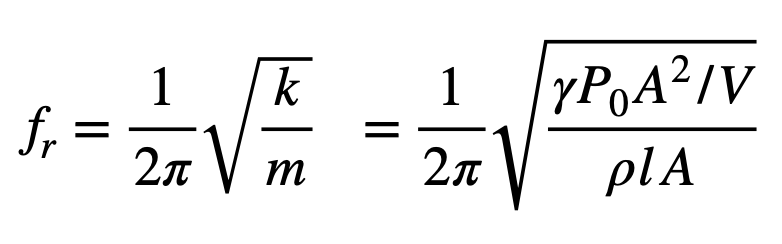
가 되고, 여기서 A 제곱과 V를 정리하면
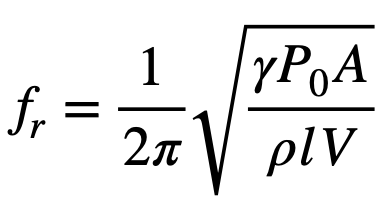
가 됩니다.
그리고 마지막으로 공기중 음속에 대한 식
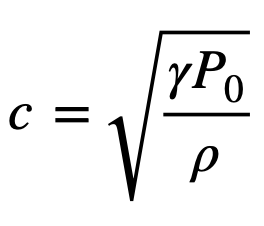
을 위 식에 대입하면,
드디어, 아름다운 헬름홀츠 공명기 공식
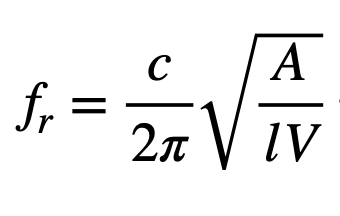
을 얻을 수 있습니다.
결론적으로 우리는 포트 단면적 A와 스피커 내부 공기의 체적 V가 어떻게 기계적 공진주파수 공식과 연결될 수 있는지 알아볼 수 있었습니다.
무엇보다도, 스프링의 공진주파수 식에서 m과 k에 해당하는 질량과 공기 스프링을 생각할 때, 포트의 단면적 A가 왜 분모가 아닌 분자에 위치하고 있는지, 유도 과정을 통해서 그 사연을 살펴볼 수 있었습니다.
읽어주셔서 감사합니다.

☕ Support my work — one coffee at a time
(Tap to buy me a coffee)
여러분의 소중한 후원은 액수에 관계 없이 측정 리뷰 및 웹사이트 운영에 큰 힘이됩니다.
웹사이트 유지를 위해 패트리온과 페이팔을 이용한 후원 방식을 고민해보았지만, 현실적으로 어려움이 있습니다.(조금 불편하시더라도 넓은 마음으로 이해 부탁드립니다.)
위 QR 코드를 통해 카카오페이로 Audio-re 를 후원하실 수 있습니다.
그리고 카카오페이 특성상 입금자명을 제외하곤 드러나는 정보가 없어, 익명을 고집하시는 것이 아니라면 감사 인사를 드릴 방법이 없습니다.
후원 후 제가 감사 인사를 드릴 수 있게 Kakao ID : seyun0915 또는
메일 주소 tpdus0915@naver.com 으로 연락 남겨주시면, 꼭 인사 드리도록 하겠습니다.
감사합니다 🙂
